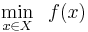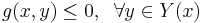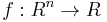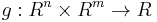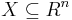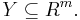Generalized semi-infinite programming

In mathematics, a semi-infinite programming (SIP) problem is an optimization problem with a finite number of variables and an infinite number of constraints. The constraints are typically parameterized. In a generalized semi-infinite programming (GSIP) problem, the feasible set of the parameters depends on the variables.^[1]

Contents

1 Mathematical formulation of the problem
2 Methods for solving the problem
3 Examples
4 See also
5 References
6 External links

Mathematical formulation of the problem

The problem can be stated simply as:

$\min\limits_{x \in X}\;\; f(x)$

$\mbox{subject to: }\$

$g(x,y) \le 0, \;\; \forall y \in Y(x)$

where

$f: R^n \to R$

$g: R^n \times R^m \to R$

$X \subseteq R^n$

$Y \subseteq R^m.$

In the special case that the set :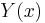 $Y(x)$ is nonempty for all 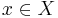$x \in X$ GSIP can be cast as bilevel programs (Multilevel programming).

Methods for solving the problem

Examples

See also

References

^ O. Stein and G. Still, On generalized semi-infinite optimization and bilevel optimization, European J. Oper. Res., 142 (2002), pp. 444-462

External links

Mathematical Programming Glossary